Bifurcation Analysis#
Bifurcation Analysis Module#
This module provides comprehensive bifurcation analysis tools for studying equilibrium dynamics, stability transitions, and parameter-dependent behaviors in adaptive environments for influencer games. It includes methods for computing equilibrium positions across parameter ranges, detecting bifurcation points, and analyzing stability properties.
The module is designed to work with the AdaptiveEnv class and provides a framework for understanding how agent behaviors and equilibrium configurations change as system parameters vary.
Dependencies:#
InflGame.adaptive.grad_func_env
InflGame.adaptive.jacobian
InflGame.utils
InflGame.kernels
InflGame.domains
Usage:#
The BifurcationEnv class can be used to analyze bifurcations and equilibrium dynamics in simulations performed using the AdaptiveEnv class. It supports various analysis types, including equilibrium bifurcation diagrams, stability analysis, and multi-order bifurcation detection.
Example:#
from InflGame.adaptive.bifurcation_analysis import BifurcationEnv
import torch
import numpy as np
# Initialize the BifurcationEnv
bif_env = BifurcationEnv(
num_agents=3,
agents_pos=np.array([0.2, 0.5, 0.8]),
parameters=torch.tensor([1.0, 1.0, 1.0]),
resource_distribution=torch.tensor([10.0, 20.0, 30.0]),
bin_points=np.array([0.1, 0.4, 0.7]),
infl_configs={'infl_type': 'gaussian'},
learning_rate_type='cosine_annealing',
learning_rate=[0.0001, 0.01, 15],
time_steps=100,
domain_type='1d',
domain_bounds=[0, 1]
)
# Set up the adaptive environment
bif_env.setup_adaptive_env()
# Compute equilibrium bifurcation diagram
equilibria = bif_env.equilibrium_bifurcation_complete(
reach_start=0.1,
reach_end=1.0,
reach_num_points=50
)
Classes
- class InflGame.adaptive.bifurcation_analysis.BifurcationEnv(num_agents, agents_pos, parameters, resource_distribution, bin_points, infl_configs={'infl_type': 'gaussian'}, learning_rate_type='cosine_annealing', learning_rate=[0.0001, 0.01, 15], time_steps=100, fp=0, infl_cshift=False, cshift=None, infl_fshift=False, Q=None, domain_type='1d', domain_bounds=[0, 1], resource_type='na', domain_refinement=10, tolerance=1e-05, tolerated_agents=None, ignore_zero_infl=False)#
Bifurcation analysis environment for studying equilibrium dynamics and stability transitions.
The BifurcationEnv class provides a comprehensive framework for analyzing bifurcation phenomena in adaptive dynamics across various domains (1D, 2D, and simplex). It supports computing equilibrium positions over parameter ranges, detecting bifurcation points of multiple orders, and analyzing stability properties through Jacobian analysis.
This class is designed to work in conjunction with the AdaptiveEnv class and provides specialized methods for understanding how system behavior changes as parameters vary, including identifying critical parameter values where qualitative changes in dynamics occur.
Methods
Compute complete equilibrium bifurcation diagram over a parameter range.
final_pos_over_reach(reach_parameters, ...)Calculate final equilibrium positions of agents over a range of reach parameters.
final_pos_over_reach_envelope(...[, ...])Calculate the envelope of equilibrium positions over a parameter range.
find_convergence_intersections(reach_parameters)Find parameter values where agent positions converge across different position variants.
find_second_order_bifs(bin_points, ...[, ...])Detect second-order (pitchfork or transcritical) bifurcation points.
find_third_order_bifurcations_refined(...[, ...])Detect third-order (subcritical or supercritical) bifurcation points with iterative refinement.
first_order_bifurcation_plot(processed_data)Generate and plot first-order bifurcation diagram with stability analysis.
learning_rate_large_end(resource_parameter)Determine appropriate learning rate upper bound for bifurcation analysis.
Set up the adaptive environment for bifurcation analysis.
- equilibrium_bifurcation_complete(reach_start=0.03, reach_end=0.3, reach_num_points=30, time_steps=100, initial_pos=None, tolerance=None, tolerated_agents=None, parallel_configs=None, envelope=False, verbose=True)#
Compute complete equilibrium bifurcation diagram over a parameter range.
This method generates a comprehensive bifurcation diagram by computing equilibrium positions across a range of reach parameter values, testing multiple initial position configurations to capture all stable equilibria. This is the primary method for creating bifurcation diagrams that visualize how equilibrium configurations change as parameters vary.
Key Features:
Proper state management with restoration after computation
Memory efficient matrix clearing between computations
Parameter validation and sensible defaults
Support for both single and envelope (max/min) equilibria
Optimized position generation for exploring initial condition space
Parallel processing support for large parameter sweeps
- Parameters:
reach_start (float) – Starting value of reach parameter range.
reach_end (float) – Ending value of reach parameter range.
reach_num_points (int) – Number of parameter values to sample in the range.
time_steps (int) – Maximum iterations for gradient ascent at each parameter value.
initial_pos (Union[List[float], torch.Tensor]) – Initial agent positions (defaults to current instance positions if None).
tolerance (Optional[float]) – Convergence tolerance (defaults to instance tolerance if None).
tolerated_agents (Optional[int]) – Convergence agent tolerance (defaults to instance value if None).
parallel_configs (Dict[str, Union[bool, int]]) – Dictionary with parallel processing configuration: {‘parallel’: bool, ‘max_workers’: int, ‘batch_size’: int}. Defaults to {‘parallel’: True, ‘max_workers’: 4, ‘batch_size’: 2}.
envelope (bool) – Whether to compute envelope (max/min) of equilibria across initial conditions.
verbose (bool) – Whether to print progress information during computation.
- Returns:
For envelope=False: torch.Tensor of shape (num_variants, num_params, num_agents). For envelope=True: List of [max_matrix, min_matrix] each of shape (num_params, num_agents).
- Return type:
Union[torch.Tensor, List[torch.Tensor]]
- final_pos_over_reach(reach_parameters, tolerance, tolerated_agents, parallel=True, max_workers=None, batch_size=None, time_steps=None)#
Calculate final equilibrium positions of agents over a range of reach parameters.
This method computes the final positions of agents by running gradient ascent via
InflGame.adaptive.grad_func_env.AdaptiveEnv.gradient_ascentfor each parameter value in the provided range. The results form the basis for bifurcation diagrams.The method has been optimized with:
Vectorized operations where possible
Parallel processing support via multiprocessing
Comprehensive error handling and input validation
Progress logging for long-running computations
Proper state preservation and restoration
- Parameters:
reach_parameters (Union[List[float], np.ndarray]) – Array of reach/influence parameter values to iterate over.
tolerance (float) – Convergence tolerance for gradient ascent at each parameter value.
tolerated_agents (int) – Number of agents allowed to violate tolerance before declaring convergence.
parallel (bool) – Whether to use parallel processing for parameter sweep.
max_workers (Optional[int]) – Maximum number of parallel workers (defaults to CPU count if None).
batch_size (Optional[int]) – Batch size for parallel processing (auto-calculated if None).
time_steps (Optional[int]) – Maximum iterations for gradient ascent (uses instance default if None).
- Returns:
Matrix of final agent positions for each parameter value (shape: len(reach_parameters) x num_agents).
- Return type:
torch.Tensor
- Raises:
ValueError – If input parameters are invalid (empty arrays, negative values, etc.).
RuntimeError – If computation fails during gradient ascent.
- final_pos_over_reach_envelope(reach_parameters, tolerance, tolerated_agents, percentage=1.0, parallel=True, max_workers=None, batch_size=None, time_steps=None, learning_rate=None)#
Calculate the envelope of equilibrium positions over a parameter range.
This method explores the envelope of possible equilibria by computing both maximum and minimum final agent positions across multiple initial conditions for each reach parameter value. This is useful for identifying regions of multistability and bifurcations where multiple equilibria coexist.
The method runs gradient ascent via
InflGame.adaptive.grad_func_env.AdaptiveEnv.gradient_ascentfrom multiple initial positions (generated by perturbing the central position) and tracks the extreme positions reached. If convergence is not achieved, the method tracks extreme positions during the specified percentage of iterations.Optimizations:
Parallel processing via multiprocessing
Vectorized operations where possible
Memory efficient computation and state management
Progress tracking for long-running computations
- Parameters:
reach_parameters (Union[List[float], np.ndarray]) – Array of reach/influence parameter values to iterate over.
tolerance (float) – Convergence tolerance for gradient ascent at each parameter value.
tolerated_agents (int) – Number of agents allowed to violate tolerance before declaring convergence.
percentage (float) – Percentage of trajectory to analyze (0.0-1.0, e.g., 0.5 for last 50%, 1.0 for entire trajectory). Controls which portion of gradient ascent history is examined for extreme values.
parallel (bool) – Whether to use parallel processing for parameter sweep.
max_workers (Optional[int]) – Maximum number of parallel workers (defaults to CPU count if None).
batch_size (Optional[int]) – Batch size for parallel processing (auto-calculated if None).
time_steps (Optional[int]) – Maximum iterations for gradient ascent (uses instance default if None).
learning_rate (Optional[List]) – Custom learning rate schedule (uses instance default if None).
- Returns:
Dictionary containing ‘max’ and ‘min’ matrices of extreme positions for each parameter. Each matrix has shape (len(reach_parameters) x num_agents).
- Return type:
Dict[str, torch.Tensor]
- Raises:
ValueError – If input parameters are invalid (empty arrays, invalid percentage range, etc.).
RuntimeError – If computation fails during gradient ascent.
- find_convergence_intersections(reach_parameters, tolerance=1e-06)#
Find parameter values where agent positions converge across different position variants.
This static method analyzes a list of equilibrium position matrices (each from different initial conditions) to identify parameter values where the equilibria from different trajectories converge to the same position within a specified tolerance. These convergence points often indicate bifurcation boundaries or transitions between different equilibrium basins.
- Parameters:
matrix_list (List[torch.Tensor]) – List of position matrices, each of shape (num_params, num_agents).
reach_parameters (torch.Tensor) – Array of parameter values corresponding to matrix rows.
tolerance (float) – Distance threshold for considering positions as converged.
- Returns:
Dictionary containing ‘convergence_points’ (parameter values where convergence occurs) and ‘parameter_indices’ (indices in reach_parameters array).
- Return type:
Dict[str, torch.Tensor]
- find_second_order_bifs(bin_points, fixed_parameters_lst, agents_pos=None, resource_distribution_type='multi_modal_gaussian_distribution_1D', alpha_st=0, alpha_end=1, varying_parameter_type='mean', learning_rate_p=[0.0001, 0.01, 100], parallel=True, max_workers=None, batch_size=None, time_steps=10000, second_run=False, data=None, num_points=100, direct_method=True)#
Detect second-order (pitchfork or transcritical) bifurcation points.
This method identifies parameter values where second-order bifurcations occur by analyzing equilibrium behavior as a resource distribution parameter varies. The method is specifically designed for three-player systems exhibiting 1-1-1 equilibrium patterns (each player at a distinct resource peak).
The algorithm systematically varies a parameter (such as mean or standard deviation of resource distribution) and identifies critical values where equilibrium structure changes qualitatively, using either direct numerical methods or root-finding approaches.
Note: This function is currently applicable only to 1-1-1 equilibria for 3 players.
- Parameters:
bin_points (Union[List[float], np.ndarray]) – Discretization points defining the domain grid.
fixed_parameters_lst (List[List[float]]) – Fixed parameters for resource distribution (e.g., means, standard deviations).
agents_pos (Optional[Union[List[float], np.ndarray, torch.Tensor]]) – Initial agent positions (defaults to instance positions if None).
resource_distribution_type (str) – Type of resource distribution function.
alpha_st (float) – Starting value of the varying parameter.
alpha_end (float) – Ending value of the varying parameter.
varying_parameter_type (str) – Which parameter to vary (‘mean’, ‘std’, etc.).
learning_rate_p (List[float]) – Learning rate parameters [min_lr, max_lr, annealing_period].
parallel (bool) – Whether to use parallel processing.
max_workers (Optional[int]) – Maximum number of parallel workers (defaults to CPU count if None).
batch_size (Optional[int]) – Batch size for parallel processing (auto-calculated if None).
time_steps (int) – Maximum iterations for gradient ascent.
second_run (bool) – Whether this is a refinement run with adjusted learning rates.
data (Optional[Union[List[float], np.ndarray, torch.Tensor]]) – Pre-computed equilibrium data to refine (used in refinement runs).
num_points (int) – Number of parameter values to sample in the search range.
direct_method (bool) – If True, uses direct gradient=0 solving with symmetric split at 0.5. If False, uses gradient ascent method to find equilibria.
- Returns:
Dictionary containing ‘sigma_star’ (bifurcation parameter values) and ‘final_parameters’ (corresponding equilibrium parameters) lists.
- Return type:
Dict[str, List]
- find_third_order_bifurcations_refined(int_position, second_order_bif, guess_distance, sig_edge, num_refinements, learning_rate_p, resource_distribution_type, varying_parameter_type, alpha_st, alpha_end, alpha_num_points, fixed_parameters_lst, learning_rate_type=None, method_type='bottom_up', parallel=True, max_workers=None, batch_size=None, time_steps=5000, verbose=True)#
Detect third-order (subcritical or supercritical) bifurcation points with iterative refinement.
This method identifies parameter values where higher-order bifurcations occur by analyzing the appearance and disappearance of equilibria as a resource distribution parameter varies. It uses an iterative refinement approach to precisely locate bifurcation points, building upon second-order bifurcation data.
The refined algorithm processes multiple resource parameters in parallel and iteratively refines bifurcation point estimates through:
Starting from second-order bifurcation estimates
Using gradient ascent from strategic initial positions
Tracking stability changes via Jacobian analysis
Iteratively refining estimates to desired precision
Optimizations:
Parallel processing using ProcessPoolExecutor
Proper state management and error handling
Memory efficient batch processing
Comprehensive logging and progress tracking
- Parameters:
int_position (torch.Tensor) – Initial position for agents.
second_order_bif (List[torch.Tensor]) – Second-order bifurcation parameters for each resource parameter.
guess_distance (torch.Tensor) – Distance parameter for initial guess estimation.
sig_edge (float) – Minimum sigma value constraint (lower bound on parameter search).
num_refinements (int) – Number of iterative refinement steps to perform.
learning_rate_p (List[float]) – Learning rate parameters [min_lr, max_lr, annealing_period].
resource_distribution_type (str) – Type of resource distribution function.
varying_parameter_type (str) – Which parameter to vary (‘mean’, ‘std’, etc.).
alpha_st (float) – Starting value of the varying parameter.
alpha_end (float) – Ending value of the varying parameter.
alpha_num_points (int) – Number of points to sample in the varying parameter range.
fixed_parameters_lst (List[List[float]]) – Fixed parameters for resource distribution.
learning_rate_type (str) – Type of learning rate schedule (uses instance default if None).
method_type (str) – Search strategy (‘bottom_up’, ‘top_down’, ‘top_down_n1’, ‘bottom_up_n1’).
parallel (bool) – Whether to use parallel processing.
max_workers (Optional[int]) – Maximum number of parallel workers (defaults to CPU count if None).
batch_size (Optional[int]) – Batch size for parallel processing (auto-calculated if None).
time_steps (int) – Maximum iterations for gradient ascent.
verbose (bool) – Whether to print progress and diagnostic information.
- Returns:
List of cycle end parameters (bifurcation points) for each resource parameter.
- Return type:
List[torch.Tensor]
- Raises:
ValueError – If input parameters are invalid (negative refinements, invalid method_type, etc.).
RuntimeError – If computation fails during bifurcation detection.
- first_order_bifurcation_plot(processed_data, infl_type='gaussian', alpha_st=0, alpha_end=1, alpha_values=None, cutoff_index=None, title_ads=[], save=False, name_ads=[], font={'cbar_size': 16, 'default_size': 24, 'font_family': 'sans-serif', 'label_size': 10, 'legend_size': 12, 'table_size': 15, 'title_size': 34}, save_types=['.png', '.svg'], paper_figure={'figure_id': 'bif_diag', 'paper': False, 'section': '3_2_6'})#
Generate and plot first-order bifurcation diagram with stability analysis.
This method creates a visualization of first-order (saddle-node) bifurcations by computing equilibrium positions and their stability across a parameter range. The plot shows how equilibrium agent positions change as a resource parameter (alpha) varies, with stability indicated through
InflGame.adaptive.jacobian.jacobian_stability_fast.The method supports both original format (e.g., Gaussian kernels) and processed data format with pre-computed stability flips, making it flexible for different analysis workflows.
First-order bifurcations are characterized by the creation or annihilation of equilibrium pairs, typically visualized as branches that meet and disappear at critical parameter values.
Example Gaussian Bifurcation Diagram
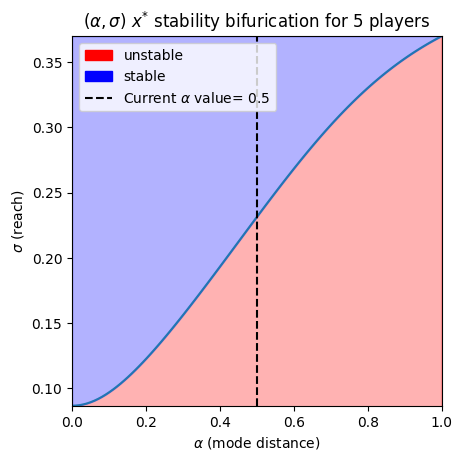
First-order bifurcation plot for 5 players using symmetric Gaussian influence kernels.#
- Parameters:
infl_type (str) – Type of influence kernel (‘gaussian’, ‘beta’, etc.).
alpha_st (float) – Starting value of the resource parameter range.
alpha_end (float) – Ending value of the resource parameter range.
processed_data (Optional[dict]) – Pre-processed bifurcation data with ‘unstable_flip’, ‘stable_flip’, and optionally ‘cycles_end’.
alpha_values (Optional[np.ndarray]) – Array of alpha (parameter) values corresponding to equilibria.
cutoff_index (Optional[int]) – Index to truncate the data (useful for focusing on specific parameter ranges).
title_ads (List[str]) – Additional text to append to plot title.
save (bool) – Whether to save the plot to file.
name_ads (List[str]) – Additional text for saved filename.
font (Dict) – Font configuration dictionary with keys: ‘default_size’, ‘cbar_size’, ‘title_size’, ‘legend_size’, ‘table_size’, ‘label_size’, ‘font_family’.
save_types (List[str]) – List of file formats for saving (e.g., [‘.png’, ‘.svg’]).
paper_figure (dict) – Configuration for paper figure saving with keys: ‘paper’ (bool), ‘section’ (str), ‘figure_id’ (str).
- Returns:
The generated matplotlib figure object.
- Return type:
matplotlib.figure.Figure
- learning_rate_large_end(resource_parameter, second_run=False, high_end=False)#
Determine appropriate learning rate upper bound for bifurcation analysis.
This method computes an appropriate maximum learning rate for gradient ascent based on the resource parameter value, with adjustments for refinement runs. The learning rate is scaled to ensure convergence while maintaining computational efficiency across different parameter regimes.
- Parameters:
resource_parameter (float) – Current value of the resource/reach parameter.
second_run (bool) – Whether this is a refinement run (uses larger learning rate if True).
high_end (bool) – Whether this is for high parameter values (further increases learning rate).
- Returns:
Computed maximum learning rate value.
- Return type:
float
- setup_adaptive_env()#
Set up the adaptive environment for bifurcation analysis.
This method initializes the gradient function environment with the provided parameters, creating an
InflGame.adaptive.grad_func_env.AdaptiveEnvinstance that will be used for equilibrium computations and bifurcation analysis.- Returns:
None